TSCTF Android Reverse - Open Sesame!
0x01 简介
如果掌握Android应用逆向分析这个技能点后,我们在遇到未知软件时就可以了解其内部逻辑。本题是我在TSCTF2019出的一道Android Reverse中等题,本题主要考察选手的知识点有:
- APK的Java和Native层的动态静态分析能力
- 常见算法(如RSA)的掌握
- 常见反调试的绕过技术
简单使用一下程序(下载地址),发现这是一个自动登录网关的程序,要求输入username、password、key即可实现自动登录网关,但是key是不知道的,这时就需要逆向分析了。
0x02 Java层分析
使用JEB分析APK后可以发现程序在Java层没有做太多的操作,对于key的校验是通过native的函数对key做check。
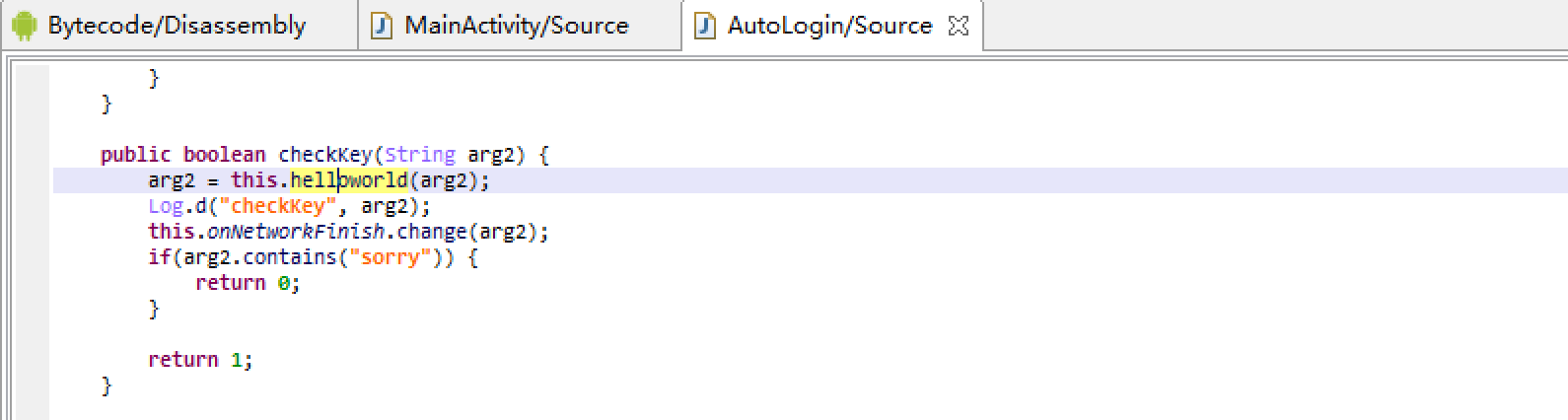
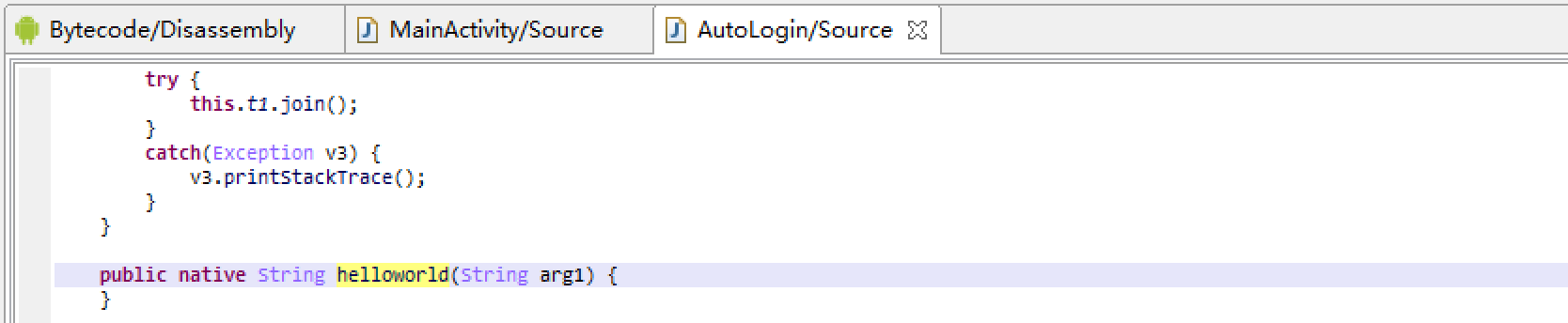
0x03 native层分析
通过静态分析程序给出的两个so文件,一个是libnative-lib.so,第二个是libnative-check.so。第一个so中只实现了一个静态注册的函数,返回一个字符串。而在第二个so中调用了JNI_Onload函数,通过查看注册的函数,发现存在对字符串加密的逻辑(寻找注册函数的方法见下文)。因此重点分析第二个so。
对于so的分析推荐使用IDA动态调试。但是在调试so时,我们会发现APK会直接退出。通过logcat --pid <pid>观察退出的日志中的关键词或者是通过在JNI_Onload下断点开始调试,都可以发现程序中加了反调试。
check逻辑
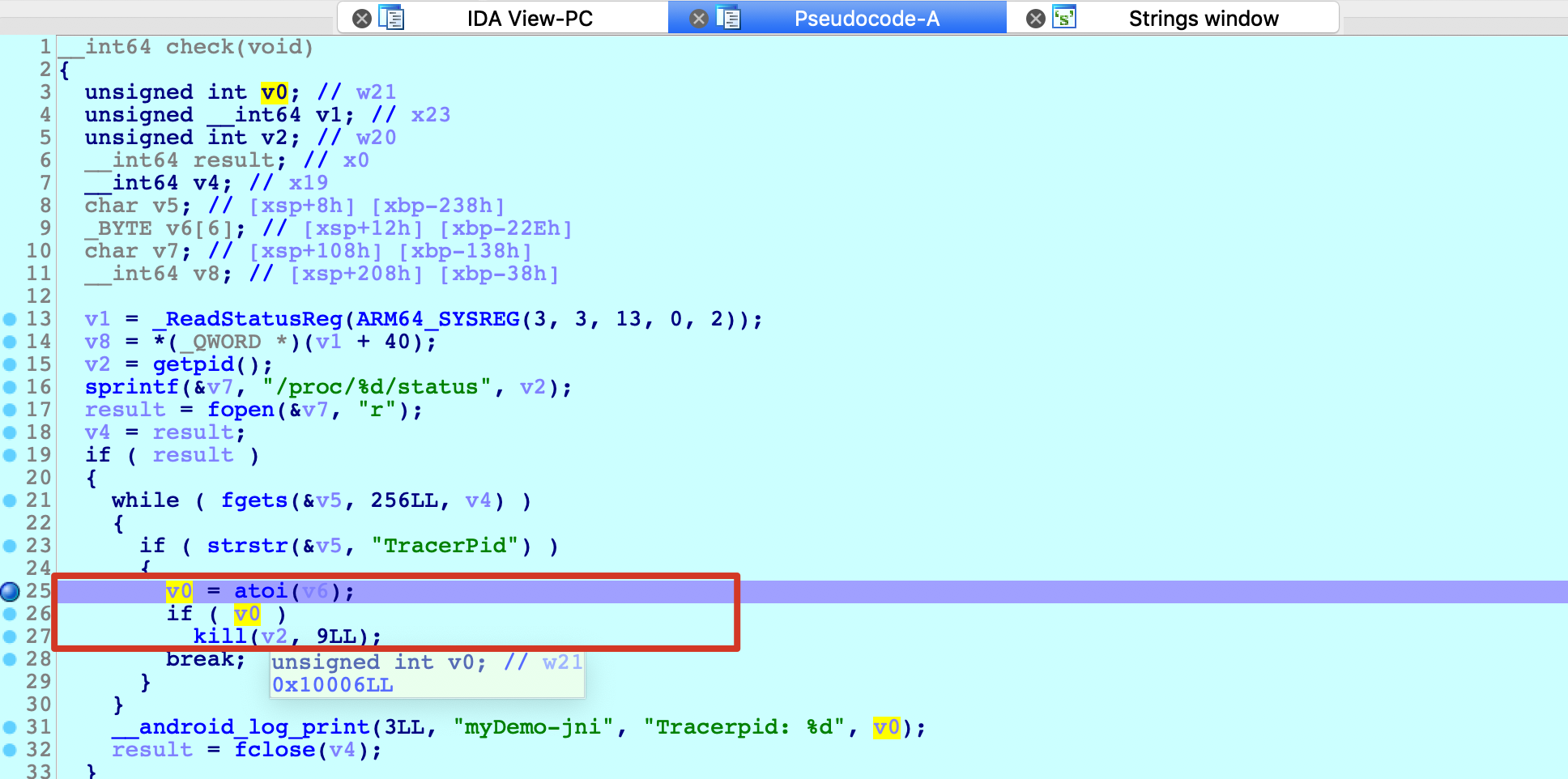
如果一个进程被调试时,/proc/<pid>/status下会记录TracerPid(调试者的pid):

check函数中就是根据这一点做了反调试:通过读取该文件,检查TracerPid是否为0,如果非0则代表被调试,kill掉程序。如下图所示,对JNI_Onload动态调试时,check函数中即将触发kill:
因此,在if判断时将v0修改为0即可绕过反调试,如下图所示,可以将W0置为0。
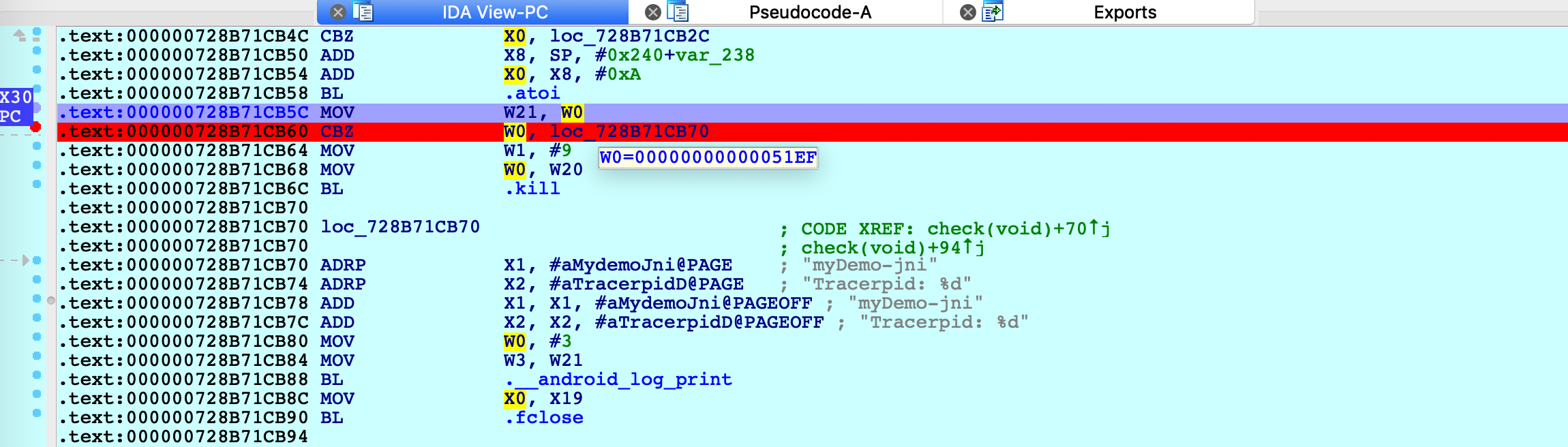
后续在encode函数中还加了一次check函数的调用,这里patch w0为其他寄存器,如w3(此时总为0),这样就可以不用每次修改寄存器的值了:
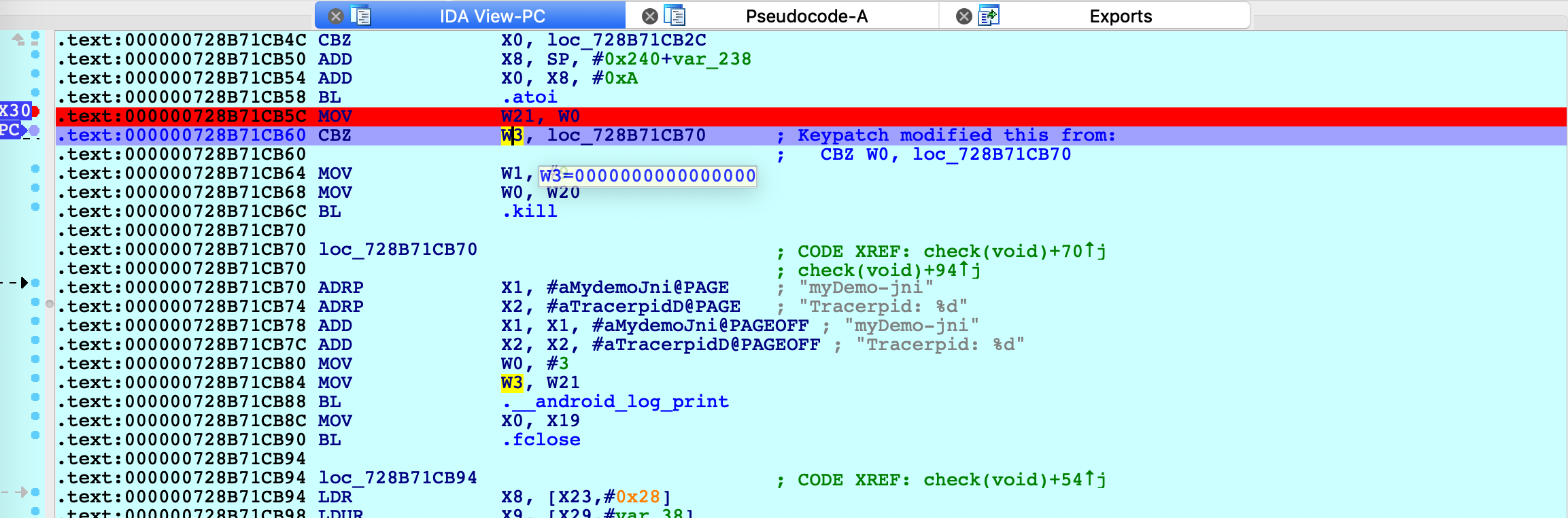
加这两个反调试的目的是为了让选手关注JNI_Onload函数中的动态注册过程找到实际的函数,以及调试程序的逻辑从而关注到后续encrypt字符串已经被修改了。反调试本身并不难,更多的反调试方法见文末的参考链接。
定位JNI_Onload中native函数
JNI_Onload函数中会实现动态注册,如何寻找到注册的是哪个函数呢?动态注册时用到的关键结构体JNINativeMethod在jni.h中,如下所示。
// jni.h
typedef struct {
const char* name; // Java层函数名
const char* signature; // 函数的参数和返回值的签名
void* fnPtr; // native层函数指针
} JNINativeMethod;
在逆向分析so时,推荐在IDA中导入jni.h头文件,并导入相关结构体,修改函数参数类型后,反编译的结果就会更加直观。导入后,在JNI_Onload函数中我们就看到RegisterNatives这个用于动态注册的函数,找到动态注册时用到的JNINativeMethod结构体成员如下:
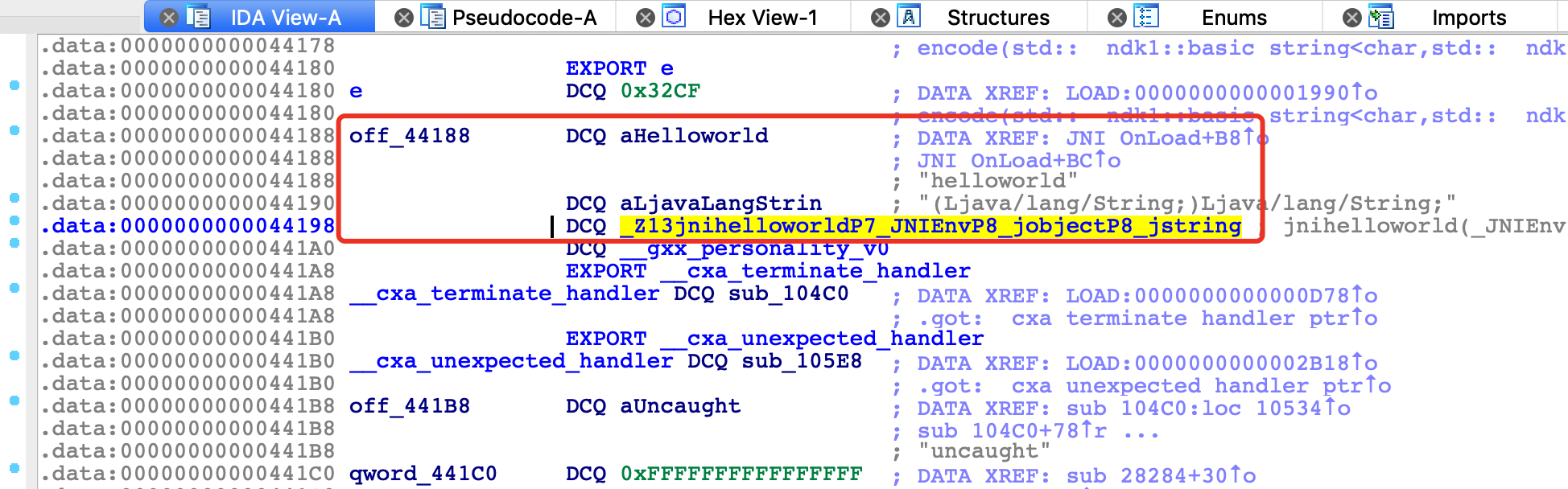
由于JNI_Onload实现了jnihelloworld函数的动态注册,我们直接分析该函数即可。该函数的逻辑很简单,我们关注最重要的部分:将用户的输入经过算法加密后和encrypt比较,如果相等则验证成功。通过分析,可以知道encrypt长度为8*0x2E。校验时反编译代码如下:
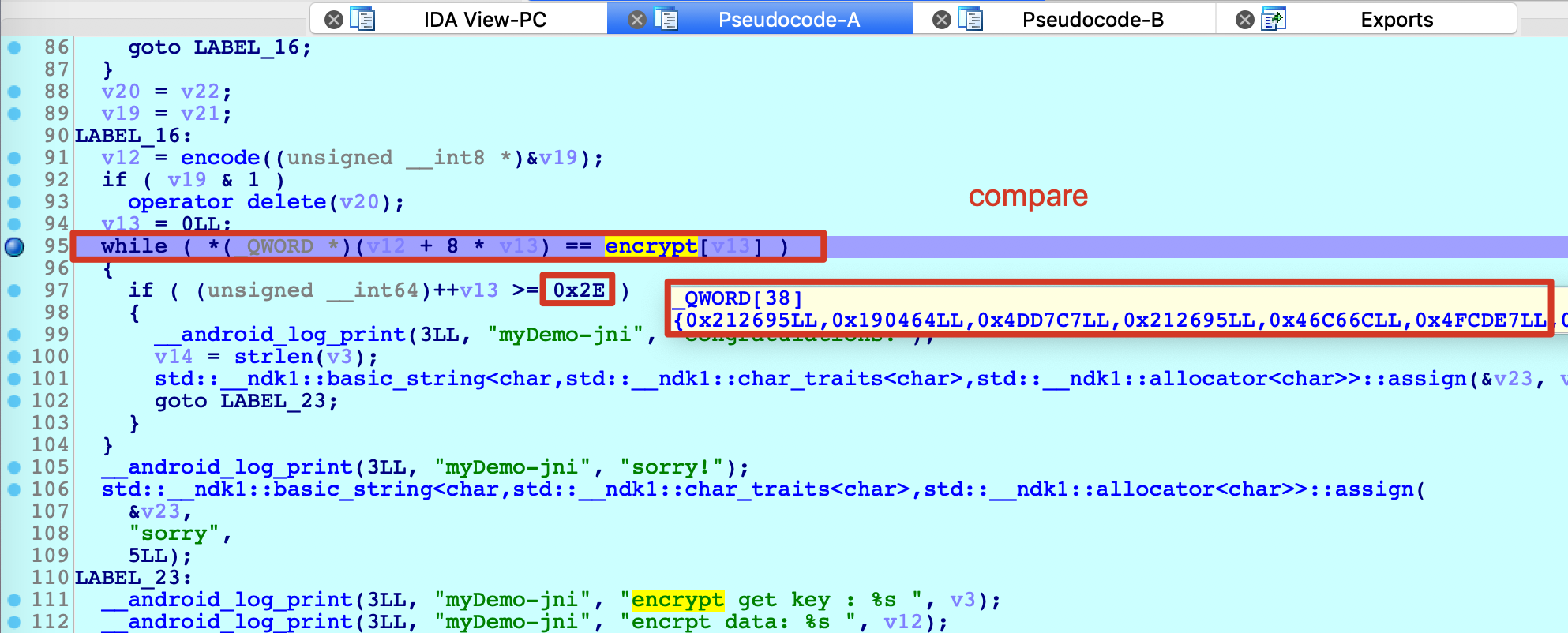
注意这里的encrypt密文字符串和原来静态文件so中是不一样的,原因在于init_array中注册了函数对该字符串做了移位操作。
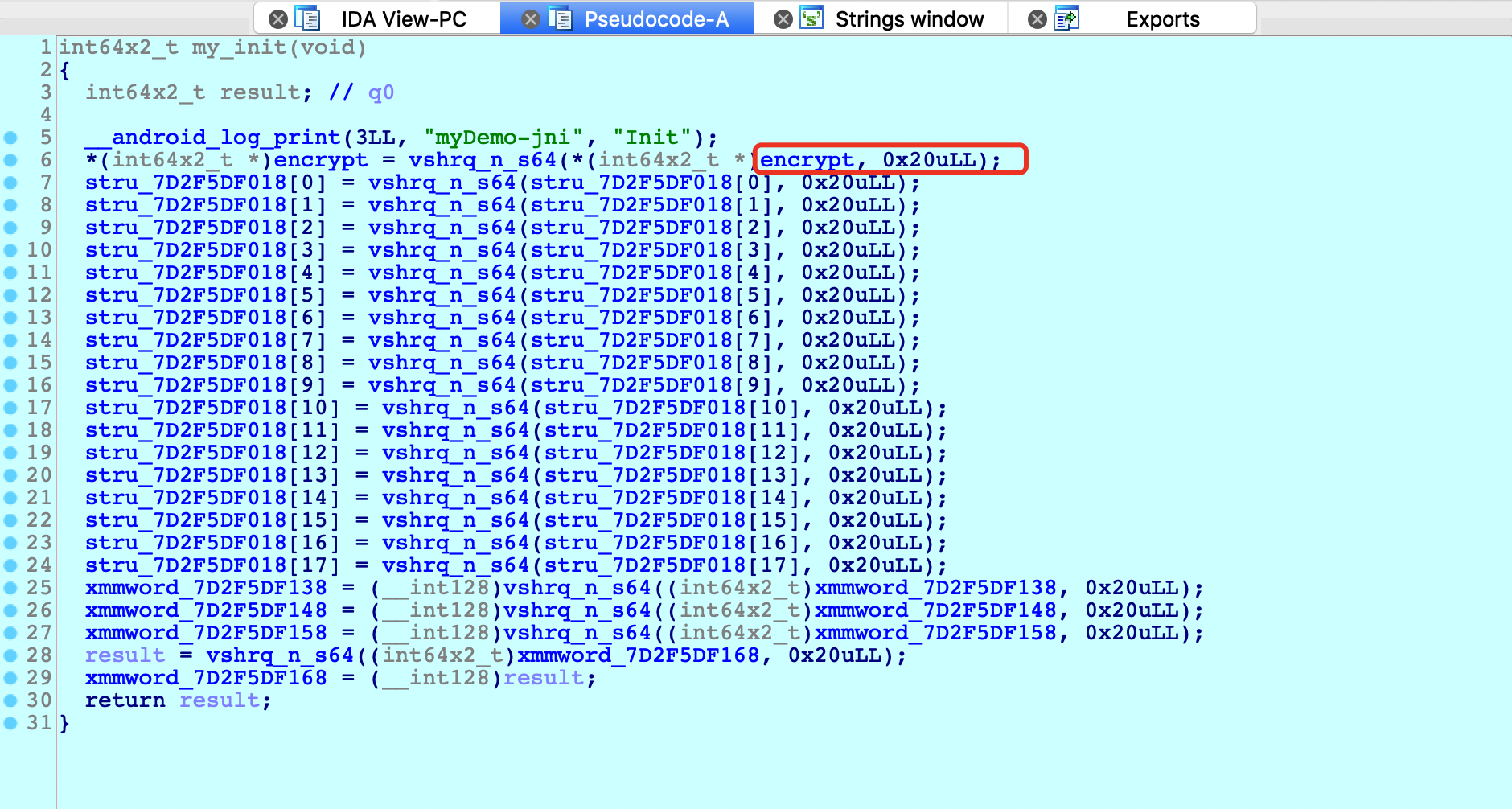
我们可以直接在动态调试时dump出encrypt的内存。IDA Python脚本如下:
# IDA Python dump memory
# Usage: Shift+F2 -> choose Python -> Paste me -> Run
import idaapi
start_address=0x0000007D2F5DF008
data_length=8*0x2E
data = idaapi.dbg_read_memory(start_address, data_length)
fp = open('/tmp/encrypt_dump', 'wb')
fp.write(data)
fp.close()
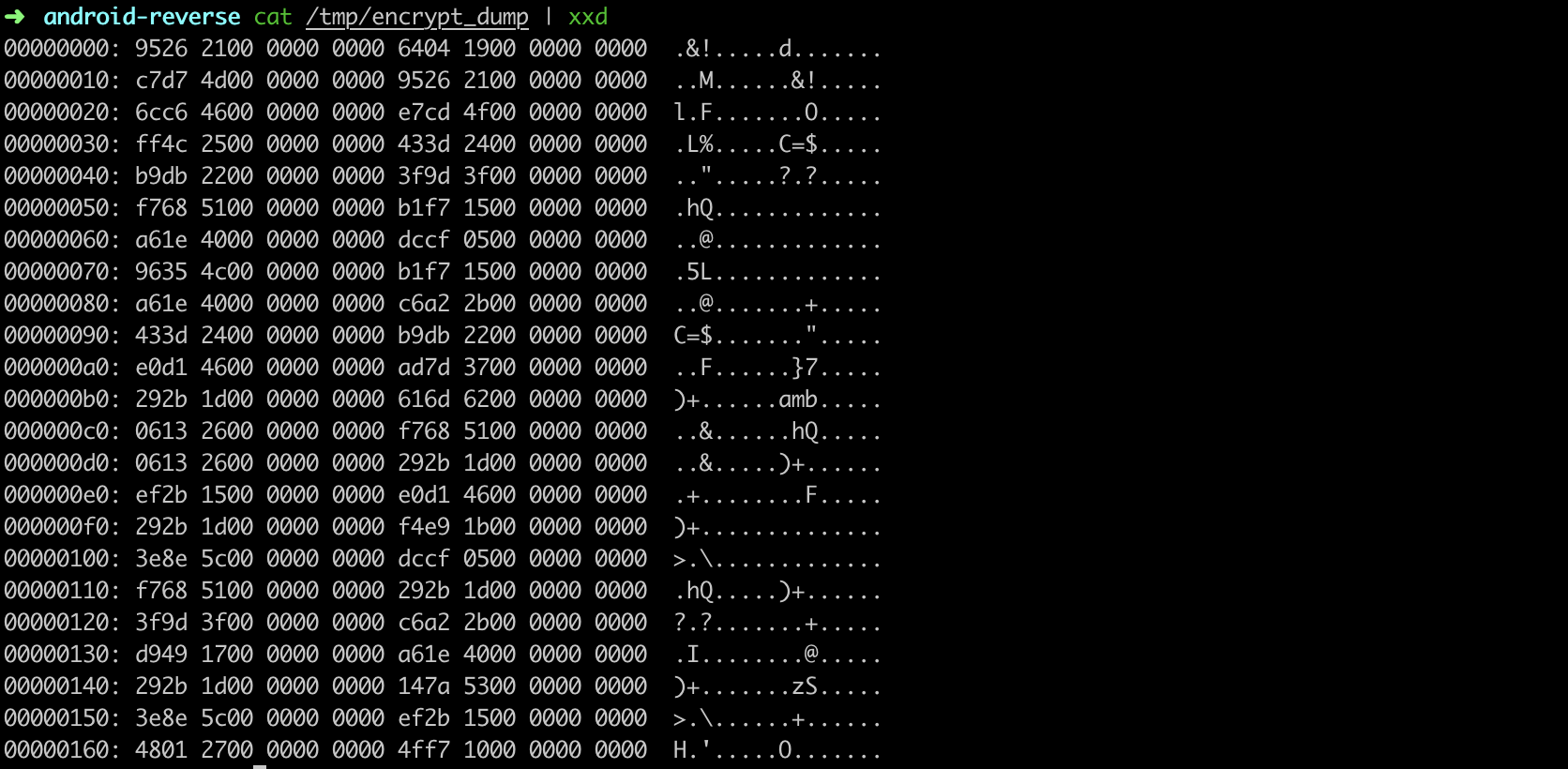
RSA 暴力破解
回溯分析加密过程,程序中在encrypt函数中完成字符串加密。通过while循环不停对输入的字符做乘方运算,并且给了明显的hint:N和e。因此可以推断出是RSA算法。

由于给了{e,N}这个公钥对,N的长度很小。因此可以暴力分解N得出p和q,计算(p-1)*(q-1)得到L,之后根据L和e求出d。得到私钥对{d, N}。由于密文已知,因此可以求出明文。
0x04 flag
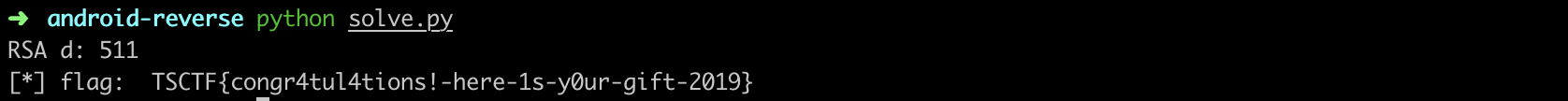
#!/usr/bin/env python
# coding=utf-8
# author: thinkycx
# date: 20190508
# Usage: to solve TSCTF Androd Reverse.
encrypt = [0x0000000000212695,0x0000000000190464,0x00000000004dd7c7,0x0000000000212695,
0x000000000046c66c,0x00000000004fcde7,0x0000000000254cff,0x0000000000243d43,
0x000000000022dbb9,0x00000000003f9d3f,0x00000000005168f7,0x000000000015f7b1,
0x0000000000401ea6,0x000000000005cfdc,0x00000000004c3596,0x000000000015f7b1,
0x0000000000401ea6,0x00000000002ba2c6,0x0000000000243d43,0x000000000022dbb9,
0x000000000046d1e0,0x0000000000377dad,0x00000000001d2b29,0x0000000000626d61,
0x0000000000261306,0x00000000005168f7,0x0000000000261306,0x00000000001d2b29,
0x0000000000152bef,0x000000000046d1e0,0x00000000001d2b29,0x00000000001be9f4,
0x00000000005c8e3e,0x000000000005cfdc,0x00000000005168f7,0x00000000001d2b29,
0x00000000003f9d3f,0x00000000002ba2c6,0x00000000001749d9,0x0000000000401ea6,
0x00000000001d2b29,0x0000000000537a14,0x00000000005c8e3e,0x0000000000152bef,
0x0000000000270148,0x000000000010f74f]
n = 6651937;
e = 13007;
# n = 1949*3413;
# e*d mod (p-1)*(q-1) = 1
for i in range(2, n):
if (e*i %( (1949-1)*(3413-1) ) ) == 1:
print "RSA d:", i
# d = 511;
break
# decrpt
flag = ''
for i in range(len(encrypt)):
result = pow(encrypt[i], 511) % n
flag += chr(result)
print "[*] flag: ", flag
# TSCTF{congr4tul4tions!-here-1s-y0ur-gift-2019}
